Alex Punnen's Home Page
Articles and Links

The Maths behind Neural Networks

Alex Punnen
© All Rights Reserved

Contents

Chapter 4

Back Propagation - Pass 1 (Chain Rule)

We have seen how gradient descent was used to optimize the cost function.

We use the method of back-propagation to propagate recursively the optimized weights from gradient descent from output layers to the input layers.

Structure of a Neural Network

Neural network is basically a set of inputs connected through ‘weights’ to a set of activation functions whose output will be the input for the next layers and so on.

neuralnetwork

For training a neural network we need a dataset which has the input and expected output. The weights are randomly initialized, and the inputs passed into the activation function and gives an output. This output or computed values can be compared to the expected value and the difference gives the error of the network. We can create a ‘Cost Function’ like what we saw in the last chapter say the Mean Squared Error. We can use the same Gradient Descent now to adjust the weights so that the error is minimized.

We do this in the last layer of the multi-layer neural network.

Now how do we adjust the weights of the inner layer ? This is where Back-propagation comes in. In a recursive way weights are adjusted as per their contribution to the output. That is weights or connections which have influenced the output more are adjusted more, than those which have influenced the output less.

How Backpropagation works

A real neural network has many layers and many interconnections. But let’s first think of a simple two layered neural network with just a linear connection between two layers, l and (l-1) to simplify the notation and to understand the maths.

\[x \rightarrow a^{l-1} \rightarrow a^{l} \rightarrow output\]

We take $a^{l}$ as the input at layer l. Input of a neuron in layer l is the output of activation from the previous layer $(l-1)$.

Output of Activation is the product of the weight w and input at layer $(l-1)$ plus the basis, passed to the activation function. We will be using the sigmoid ($\sigma$ ) function as the activation function.

Writing this below gives.

\[a^{l} = \sigma(w^l a^{l-1}+b^l).\]

(Same notation as in http://neuralnetworksanddeeplearning.com/chap2.html)

Let the expected output be $y$ for a training example $x$. Notice that we train with a lot of examples. But we are talking here now about only one example in the training set for simplicity.

The calculated output for a network with $l$ layer is $a^l$.

Let’s calculate then the loss function. Difference of expected to the calculated.

Let’s use the quadratic cost function here.

\[C = \frac{1}{2} \|y-a^L\|^2\]

If there are $j$ output layers, we need to take the sum of all the activations of the $j$ layers as below. The above is more simplified version.

\[C = \frac{1}{2} \sum_j (y_j-a^L_j)^2\]

Now this Cost needs to be reduced. We can use the gradient descent to find the path to the optimal weight that reduces the cost function for a set of training examples.

As we have seen earlier in gradient descent chapter, we get the path to the optimal weight by following the negative of the gradient of the Cost function with respect to the weight. But in multi-layered neural network the question gets tricky on how to update the weights in the different layers. This is where Backpropagation algorithm comes in.

Back-Propagation

Speaking generally, it is the mechanism to adjust the weights of all the layers according to how strong was each of their influence on the final Cost.

More specifically - It is an algorithm to adjust each weight of every layer in a neural network, by using gradient descent, by calculating the gradient of the Cost function in relation to each weight.

Back-Propagation in Detail

Consider a neural network with multiple layers. The weight of layer $l$ is $w^l$. And for the previous layer it is $w^{(l-1)}$.

The best way to understand backpropagation is visually and by the way it is done by the tree representation of 3Blue1Brown video linked here.

The below GIF is a representation of a single path in the last layer($l$ of a neural network; and it shows how the connection from previous layer - that is the activation of the previous layer and the weight of the current layer is affecting the output; and thereby the final Cost.

The central idea is how a small change in weight affects the final Cost in this chain depiction.

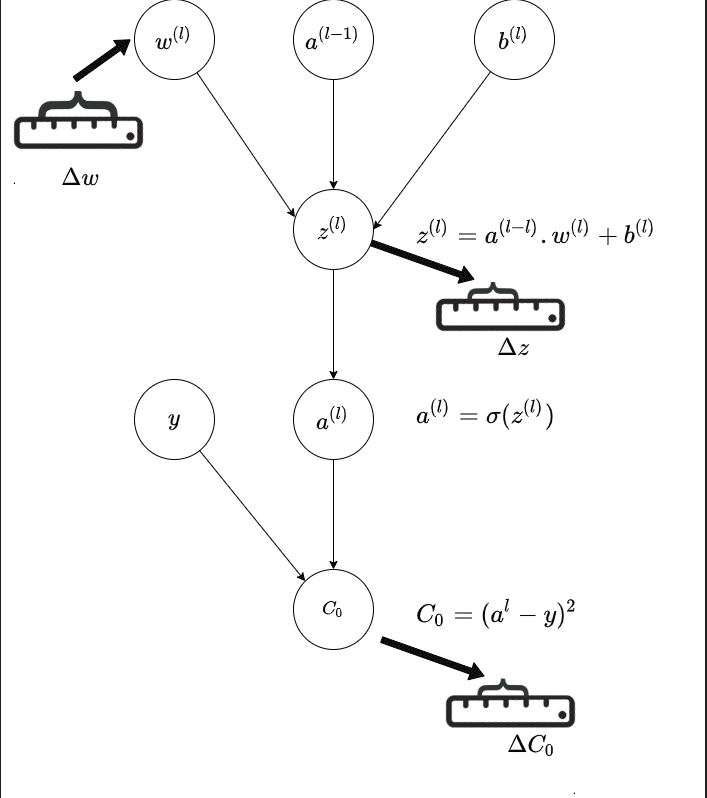backpropogationgif Source : Author

Chain Rule of Calculus and Back Propogation

Here is a more detailed depiction of how the small change in weight adds through the chain to affect the final cost, and how much the small change of weight in an inner layer affect the final cost.

This is the Chain Rule of Calculus and the diagram is trying to illustrate that visually via a chain of activations, via a Computational Graph

\[\delta C_0/\delta w^l = \delta z^l/\delta w^l . \delta a^l/\delta z^l . \delta C_0/\delta a^l\]

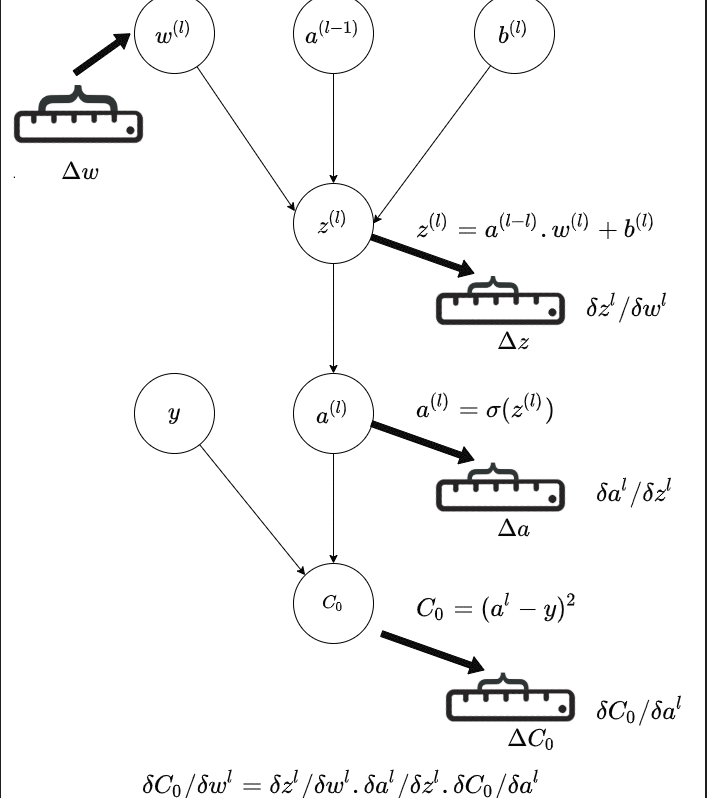backpropogationgif2 Source : Author

Next part of the recipe is adjusting the weights of each layers, depending on how they contribute to the Cost.

Neurons that fire together, wire together. This is what we are doing with gradient descent and back propogation. Strengthening the stronger links and weakening the weaker links, vaguely similar to how biological neurons wire together.

The weights in each layer are adjusted in proportion to how each layers weights affected the Cost function.

This is by calculating the new weight by following the negative of the gradient of the Cost function - basically by gradient descent.

\[W^l_{new} = W^l_{old} - learningRate* \delta C_0/ \delta w^l\]

For adjusting the weight in the $(l-1)$ layer, we do similar

First calculate how the weight in this layer contributes to the final Cost or Loss

\[\delta C_0/\delta w^{l-1} = \delta z^{l-1}/\delta w^{l-1} . \delta a^{l-1}/\delta z^{l-1} . \delta C_0/\delta a^{l-1}\]

and using this. Basically we are using Chain rule to find the partial differential using the partial differentials calculated in earlier steps.

\[W^{l-1}_{new} = W^{l-1}_{old} - learningRate* \delta C_0/ \delta w^{l-1}\]

Next would be to add more layers and more connections and change the notation to represent the place of each weight in each layer so $w^l$ becomes $w^l_{j,k}$

weightnotation Source : Michael Nielsen: NeuralNetwork and Deep Learning book

This is the first pass; there are more details now to fill in; which we will take in subsequent chapters.

Next: Back propagation - Pass 2 (Scalar Calculus)

References

http://neuralnetworksanddeeplearning.com/chap2.html

https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/